Reasoning about experiments (Backdoors and adjustments)

The following example is discussed as Example 3.4 in Chapter 3-4 (http://bayes.cs.ucla.edu/BOOK-2K/ch3-3.pdf). See also http://causality.cs.ucla.edu/blog/index.php/category/back-door-criterion/.

The causal model we are going to study can be represented using the following DAG concerning a set of variables numbered 1 to 8:

using CausalInference
using TikzGraphs
# If you have problems with TikzGraphs.jl,
# try alternatively plotting backend GraphRecipes.jl + Plots.jl
# and corresponding plotting function `plot_pc_graph_recipes`


dag = digraph([
    1 => 3
    3 => 6
    2 => 5
    5 => 8
    6 => 7
    7 => 8
    1 => 4
    2 => 4
    4 => 6
    4 => 8])
t = plot_pc_graph_tikz(dag)

We are interested in the average causal effect (ACE) of a treatment X (variable nr. 6) on an outcome Y (variable nr. 8), which stands for the expected increase of Y per unit of a controlled increase in X. Variables nr. 1 and nr. 2 are unobserved.

Regressing Y (nr. 8) on X (nr. 6) will fail to measure the effect because of the presence of a confounder C (variable nr. 4), which opens a backdoor path, a connection between X and Y via the path 6 ← 4 → 8 which is not causal.

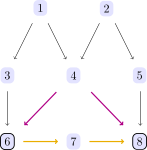
We can avert such problems by checking the backdoor criterion. Indeed

backdoor_criterion(dag, 6, 8) # false

reports a problem.

One might want to condition on the confounder C (nr. 4)` to obtain the causal effect, but then

backdoor_criterion(dag, 6, 8, [4]) # still false

there is still a problem ( because that conditioning opens up a non-causal path via 6 ← 3 ← 1 → 4 ← 2 → 5 → 8.)

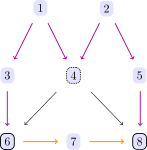
But conditioning on both Z = [4, 5] solves the problem, as verified by the backdoor criterion.

backdoor_criterion(dag, 6, 8, [3, 4]) # true
backdoor_criterion(dag, 6, 8, [4, 5]) # true

(also conditioning on Z = [3, 4] would be possible.)

Thus, regressing Y on X and controlling for variables numbered Z = [4, 5] we measure the average causal effect.

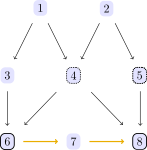
What we have done by hand here is the search for an backdoor adjustment set. We could have directly queried

Zs = list_covariate_adjustment(dag, 6, 8, Int[], setdiff(Set(1:8), [1, 2])) # exclude variables nr. 1 and nr. 2 because they are unobserved.

which lists possible adjustment sets,

println.(Zs);

    Set([4, 3])
    Set([5, 4])
    Set([5, 4, 3])

to get the list of possible adjustment sets. Here list_backdoor_adjustment gives adjustment sets for a backdoor criterion similar to backdoor_criterion and list_covariate_adjustment the more versatile adjustment set based on the sound and complete graphical criterion for covariate adjustment given in [https://arxiv.org/abs/1203.3515] using the algorithmic approach proposed in [https://arxiv.org/abs/1803.00116].